PageRank

PageRank는 상당히 직관적이고 간단하게 이해할 수 있는 개념이지만 그 이면을 들여다 보면 공부할 만한 사실들이 상당히 많이 있다. 그 중 중요하다고 생각하는 부분들에 대해서 소개하려고 한다.

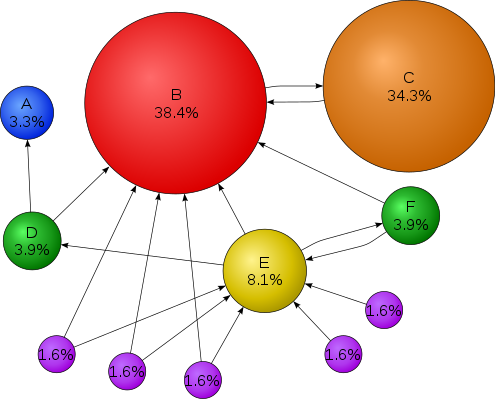
graph theory에서 graph상에서 node의 증요도를 측정하는 것은 상당히 중요한 부분이다. 이것을 centrality를 측정한다라고 하는데, PageRank는 웹이라는 거대한 그래프 상에 존재하는 페이지 하나하나를 node로 하여 node의 eigenvector centrality를 측정하는 방식이라고 할 수 있다. 이 부분에 대해 설명하기 전에 먼저 PageRank 자체에 대해 알아보기로 하자.

PageRank는 다음과 같은 가정으로 웹페이지의 중요도를 계산한다.

1. 다른 페이지로 이동할 수 있는 link를 많이 포함하고 있는(outbound link가 많은) 페이지는 상대적으로 중요도가 낮다
   • 예를 들면, sitemap을 담고 있는 페이지나, 포털과 같은 페이지는 다른 페이지로 건너 가기 위한 수단이 되는 페이지이므로 상대적으로 중요한 정보를 담고 있지 않다고 가정한다.
2. 다른 페이지의 link로 부터 유입되기 쉬운(inbound link가 많은) 페이지는 상대적으로 중요도가 높다.
   • 전문적인 지식을 담고 있는 블로그나 중요한 뉴스 기사는 다른 페이지로부터 참조될 소지가 많다.

이러한 가정을 담은 식을 아래와 같이 표현 할 수 있다.

$$PR(u) = \sum_{v \in B_u} \frac{PR(v)}{L(v)},$$

• $PR(u)$: 페이지 u의 중요도 (u의 페이지랭크 값)
• $B_u$: 페이지 u로 link를 가진 모든 페이지 집합
• $L(v)$: 페이지 v의 outbound link 수

따라서 페이지 u의 중요도, $PR(u))$는 페이지 u로의 link를 가지고 있는 모든 페이지 v의 중요도, $PR(v))$의 합산으로 (단, $L(v)$로 나누는 방식으로 패널티를 주어) 표현한다.

하지만 PageRank의 실제 식은 다음과 같은데,

$$PR(p_i) = \frac{1-d}{N} + d \sum_{p_j \in M(p_i)} \frac{PR (p_j)}{L(p_j)}$$

• $N$: 전체 페이지 수

이는 페이지 $p_i$의 중요도, $PR(p_i)$ 값은 $\cfrac 1 N$과 $\sum_{p_j \in M(p_i)} \frac{PR (p_j)}{L(p_j)}$을 $1-d : d$의 비율로 가중합 하여 계산하였다.

어쩌면 이 부분 때문에 PageRank가 이론적으로 굉장히 탄탄한 배경을 가지고 있다고 볼 수 있는데, 좀 더 자세한 해석을 위해 위 식을 다음과 같이 행렬 표현식으로 바꾸어 보자.

$$\small{ \begin{bmatrix} PR(p_1)^{(i+1)} \\ PR(p_2)^{(i+1)} \\ \vdots \\ PR(p_N)^{(i+1)} \end{bmatrix} = \begin{bmatrix} {(1-d)/ N} \\ {(1-d) / N} \\ \vdots \\ {(1-d) / N} \end{bmatrix} + d \begin{bmatrix} \ell(p_1,p_1) & \ell(p_1,p_2) & \cdots & \ell(p_1,p_N) \\ \ell(p_2,p_1) & \ddots & & \vdots \\ \vdots & & \ell(p_i,p_j) & \\ \ell(p_N,p_1) & \cdots & & \ell(p_N,p_N) \end{bmatrix} \begin{bmatrix} PR(p_1)^{(i)} \\ PR(p_2)^{(i)} \\ \vdots \\ PR(p_N)^{(i)} \end{bmatrix} }$$

• $PR(p)^{i}$: i번째 iteration에서의 페이지 p의 패이지랭크 값
• $\ell(p_i, p_j)$: 페이지 j에서 페이지 j로의 outbound link 갯수 / 페이지 j의 총 outbound link 갯수 $\bigg(\sum_{i = 1}^N \ell(p_i,p_j) = 1\bigg)$

위와 같이 표현 했을 때 알 수 있는 중요한 사실은,

$\mathbf{R} = \begin{bmatrix} PR(p_1) \\ PR(p_2) \\ \vdots \\ PR(p_N) \end{bmatrix}$ 은 eigenvector 라는 사실이다.

그 이유는, 위 식 2를 다시 아래와 같이 정리할 수 있다.

$$\begin{aligned} \mathbf{R}^{(i+1)} &= \frac{1-d}{N} \mathbf{1} + d \cdot \mathcal{A} \cdot \mathbf{R}^{(i)} \\ &= \left(\frac{1-d}{N} \mathbf{E} + d \cdot \mathcal{A} \right)\mathbf{R}^{(i)} =: \widehat{ \mathcal{A}} \cdot \mathbf{R}^{(i)} \end{aligned}$$

• $\mathbf{1}$: 1로 이루어진 column vector
• $\mathcal{A}$: Adjecent Matrix (이 경우 각 컬럼의 합이 1이므로 stochastic matrix)
• $\mathbf{E}$: 단위 행렬 (단위 행렬은 당연히 stocahsitic matrix)
  • $\mathbf{R}$ 벡터를 propbability distribution로 생각하기 때문에, $\mathbf{E} \cdot \mathbf{R} = \mathbf{1}$

$$\mathbf{Ax} = {\lambda}\mathbf{x}$$

• $\mathbf{x}$: eigenvector
• $\lambda$: eigenvalue

결론적으로 식 3은 식 4의 형태를 가지게 되고, 인접 행렬이 변형된 $\mathcal{A}$ 행렬이 transition propbablity의 성격을 갖는다면, 즉 stochastic probability라면 eigenvalue가 단위 행렬 형태로 갖게 된다고 생각 할 수 있기 때문에, 패이지랭크 벡터 $\mathbf{R}$은 식 2에서 표현한 것처럼 iterative하게 계산 될 수 있다. 이것을 power iteration(혹은 power method)라 한다.

특히 인접 행렬이 변형된 $\mathcal{A}$ 행렬을 살펴보면, 자기 자신으로 transition 될 확률을 최소한 $\cfrac {1-d} N$ 만큼 보장 받게 된다. 이것은 damping factor라고 불리는 $d$라는 값 덕분에 웹사이트를 돌아다니는 random suffer가 어떤 노드에 정착해서 빠져나올 수 없는 상황을 방지하게 되는 역할을 한다.

여기서 잠깐 PageRank를 좀 더 직관적으로 생각해 본다면, 웹서핑을 하는 사람이 랜덤으로 페이지에 있는 링크를 클릭하고, 클릭하고, ..., 클릭하고 를 무한히 반복한 다고 할때, 많이 방문하게 되는 페이지가 중요도가 높은 페이지라고 생각할 수 있는데, 이것은 인터넷에 존재하는 각 페이지들을 state로 하는 Markov Chain으로 볼 수 도 있다.

Markov Chain 관점에서 PageRank를 설명할 때 damping factor의 역할은, 각 페이지들을 state로 하는 Markov Chain에 erogodic한 속성을 부여해줌으로써, 각 노드의 중요도로 표현되는 PageRank 값은 아래와 같은 balance equestion을 통해 limiting distribuiton을 가진 벡터로 계산 될 수 있다.

$$\pi = \pi P$$

• $\pi$: limiting probabilty
• $P$: Markov Chain (transition probability 행렬)